Реализация межпредметных связей отдельных разделов алгебры и начал математического анализа

Еще в Древнем мире было широко распространено ростовщичество - дача денег в долг под процент. В Древнем Вавилоне Лихва составляла до 20% в год. При этом, если должник не возвращал вовремя долг, на следующий год проценты начислялись уже не только на основную сумму долга, но и на наросшие проценты и т. д. Во многих случаях это приводило к тому, что должник оказывался несостоятельным и попадал в рабство.

Рассмотрим задачу:

Взята в долг сумма а рублей. Какую сумму надо отдать через n лет, если деньги взяты под р % в год?

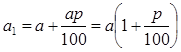Ясно, что за первый год нарастает сумма равна и общая сумма долга равна (рублей). На второй год проценты начисляются уже на сумму 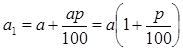и составляют сумму 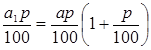, а потому общая сумма долга равна: 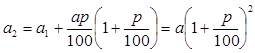. Аналогично, к концу третьего года долг будет составлять 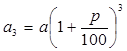, четвертого: 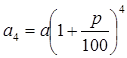. Вообще через n лет сумма долга составит: .

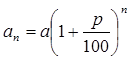Полученное равенство называют формулой сложных процентов.

Эту формулу применяют для вычисления суммы и в том случае, когда число протекших лет не является целым. Именно, через х лет надо выплатить сумму 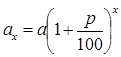рублей.

При а=1 эта формула принимает вид: и задает показательную функцию с основанием: .

При р=100 имеем .

Предположим теперь, что начисление процентов происходит не ежегодно, а ежемесячно, но зато процентная ставка в 12 раз меньше. Тогда через х лет сумма долга будет выражаться формулой 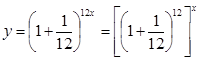.Вычисления показывают, что Если начисление процентов будет производиться ежедневно, но процентная ставка будет в 365 раз меньше (29 февраля начисления не производятся), то через х лет сумма долга будет выражаться формулой: 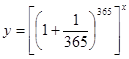. Вычисления показывают, что: .

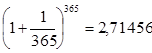Это значение весьма близко к значению числа е. Можно показать, что по увеличению n значение числа приближается к е.

Другие примеры применения показательной и логарифмической функции в различных областях знаний представлены в приложении 1 .

Использование таких примеров полезно при введении понятия показательной и логарифмической функции и их свойств.

Учащиеся отвлекаются от сухого изложения материала, формул, которые просто заучивают наизусть, не понимая зачем. Такие примеры позволяют осмысленно применять знания и, пожалуй, самое главное, делают изучение математики интереснее и легче.

Другое о педагогике:

Прорыв или тупик
Оптимистическое видение современной эпохи рядоположенно с глобальными проблемами усматривает черты прорыва к новым измерениям прогресса цивилизации. Отмечается устремление политиков к новому международному порядку, основанному на этике солидарного развития и ведущему к безопасному ненасильственному ...

Методические рекомендации для повышения уровня ответственности детей группы риска
Работа по повышению уровня ответственности должна проходить по двум направлениям: 1) формирование представлений детей об ответственности; 2) упражнение, тренировка в проявлении ответственности. Занятия с детьми рекомендуется проводить через день в течение 3 месяцев на базе реабилитационного центра. ...

Работа с трудными подростками и решение проблемы беспризорности в России в 20–30-х гг. ХХ в
В 20-е – начало 30-х гг. ХХ века складывались концептуальные подходы к работе с трудными подростками, основополагающими среди которых можно назвать следующие принципы: · принцип трудового воспитания бездомных детей. Труд не просто как средство занять детей и дать определенные знания, умения и навык ...