Реализация межпредметных связей отдельных разделов алгебры и начал математического анализа

Ответ: 20, 40.

Примеров таких задач множество, особенно применительно к задачам экономического содержания. Приведем пример. Функция прибыли фирмы имеет вид: П(Q)=R(Q) – C(Q)=2/5 Q2 – 4Q + 20, где R(Q) – выручка, C(Q) - издержки. Сколько следует фирме производить продукции, если ее производственные мощности ограничены объемом производства Q = 3.

Решение.

Задача сводиться к исследованию функции на наибольшее значение на промежутке [0;3].

П´(Q) = 4/5 Q – 4

П´(Q) = 0

Q = 5

Таким образом, Q = 5 – критическая точка. Проанализируем характер изменения производной (Рис. 4)

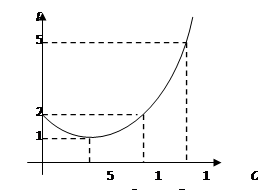
Рис.4

При Q < 5 П´(Q) < 0 и прибыль убывает; при Q > 5 П´(Q) > 0 и прибыль возрастает. Следовательно, в точке экстремума прибыль принимает минимальное значение, и таким образом этот объем производства не является оптимальным. Точка Q = 5 не принадлежит промежутку [0;3], и функция на нем убывает, следовательно, она принимает наибольшее значение при Q = 0. В этом случае при Q = 3, фирме выгодно ничего не производить (например, сдавать помещение в аренду) .

Рассмотрим, как возможно реализовать межпредметные связи на основе задачного материала. Здесь при составлении системы задач нужно учитывать принципы, выделенные в I главе. Особое значение имеют принципы преемственности, связи теории с практикой и принцип полноты. На отработку данной темы в классах гуманитарного профиля можно предложить различные прикладные задачи, в том числе социально-экономического содержания. Содержательная сторона задач должна соответствовать реальной действительности, отвечать интересам учеников, можно использовать историко-научный материал. Например:

Легенда об основании Карфагена гласит, что когда финикийский корабль пристал к берегу, местные жители согласились продать прибывшим столько земли, сколько можно оградить бычьей шкурой. Но хитрая финикийская царица Дидона разрезала эту шкуру на ремешки, связала их и оградила ремнем большой участок земли, примыкавший к морю. Считая берег моря прямолинейным, а огражденный участок прямоугольным, перед Дидоной встала задача: как оградить прямоугольный участок имеющимися ремешками длиной l, чтобы площадь была наибольшей?

База находится в лесу в 5 км от дороги, а в 13 км от базы на этой дороге есть железнодорожная станция. Пешеход по дороге идет со скоростью 5 км/ч, а по лесу – 3 км/ч. За какое минимальное время пешеход может добраться от базы до станции?

Командиру межгалактического космического корабля, движущемуся по закону x(t)=1+9t+3t2-t3 , сообщили о том, что приборы зафиксировали неопознанный летающий объект, стремительно приближающийся к кораблю. Чтобы избежать столкновения, необходимо максимально увеличить скорость. Каким должно быть ускорение корабля в момент, когда скорость станет максимальной?

Задача из истории математики, которую Евклид решал чисто геометрическим методом: доказать, что из всех параллелограммов, вписанных в данный треугольник, наибольшую площадь имеет тот, основание которого равно половине основания треугольника.

Для решения задач на оптимизацию желательно вместе с учащимися составить алгоритм, который совмещал бы в себе схему решения задач методом математического моделирования и алгоритм нахождения наибольшего (наименьшего) значения непрерывной функции. Действовать по алгоритму учащимся-гуманитариям проще, к тому же алгоритмы помогают свертывать рассуждения, избегать многословности.

Другое о педагогике:

Условия развития креативности младших школьников на уроках физкультуры
Реализуя принцип сознательности и активности, следует воспитывать у занимающихся креативное отношение к процессу физического воспитания, инициативу и самостоятельность. Это магистральный путь, способствующий достижению высоких результатов на каждом занятии и внедрению физической культуры в быт. Осн ...

Интегрированные занятия
В настоящее время интегрированные занятия в дошкольных учреждениях стали пользоваться большой популярностью. Интеграция — это система, предлагающая объединение, соединение, сближение учебного материала отдельных курсов в единое целое. Интегрированное занятие — это занятие, которое базируется на осн ...

Контрольный эксперимент и его анализ
По окончании формирующего (обучающего) эксперимента нами был проведен контрольный эксперимент. Контрольное задание показало, что практически у большинства детей экспериментальной группы с задержкой психического развития повысилась успешность и качество выполнения заданий. Так, в первом задании на с ...