Реализация межпредметных связей отдельных разделов алгебры и начал математического анализа

Производная - одно из фундаментальных понятий математики. Основной целью проведения занятий элективного курса является показать широкое применение производной в различных науках (математике, физике и технике, естествознании и химии, сельском хозяйстве и военном деле, экономике).

В математике производная применяется для вычисления производной, исследования функций, в практических задачах оптимизации.·В физике с помощью производной находится сила, мощность, масса тонкого стержня, сила тока, скорость и ускорение, теплоёмкость.·В химии и естествознании – для нахождения дозы лекарства, при которой побочный эффект будет минимальным, а реакция максимальной.·В экономике – для анализа производственных функций, широко используемых в современных экономических исследованиях.

Кратко охарактеризуем этот курс. Элективный курс является предметным с практической направленностью, цель которого – повторение, углубление и обобщение материала, расширение кругозора учащихся, более подробное рассмотрение вопросов, связанных с применением производной в других науках, использования производной для исследования функций и решения задач на оптимизацию. Но так как курс рассчитан для проведения в гуманитарных классах, то в нем достаточно большую часть занимает материал прикладного характера, то есть, обращение к историческим фактам, решение практических, занимательных задач. Вернемся к главному вопросу - реализации межпредметных связей в рамках этого курса.

Рассмотрим применение выделенных в Главе II §2, п. 2.1 трех способов.

На занятии об истории возникновения понятия производной можно привести следующий материал. Одной из важных предпосылок появления дифференциального исчисления стали практические задачи нахождения кратчайшего пути. Первые задачи на максимум и минимум были поставлены в V веке до н.э. Эти задачи решали Евклид, Архимед, Кеплер, Герон, Ферма. Общие методы не были разработаны, каждая задача решалась индивидуально. Ферма установил, что свет в неоднородной среде движется вдоль такой траектории, чтобы время прохождения пути было наименьшим. В XVII веке были разработаны общие методы решения задач на экстремум Ньютоном и Лейбницем.

Подробный материал об этих открытиях могут подготовить и сами учащиеся.

Важным моментом является показ практического применения производной.

Подробнее можно рассмотреть следующие примеры.

Бумажный змей

Бумажному змею, имеющему форму кругового сектора, желают придать такую форму, чтобы он вмещал в данном периметре р = 80 см наибольшую площадь. Каковы должны быть размеры бумажного змея?

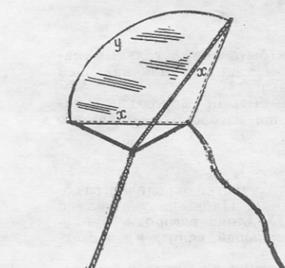
Рис.3

Решение.

Введем обозначения (рис.3):

Пусть радиус сектора – х, дугу обозначим за у, тогда периметр можно выразить так: и площадь равна: . Выразим и подставим в формулу площади: . Найдем производную функции S:

Исследуем функцию на интервале (0 ; 80). Получаем, что в точке функция принимает наибольшее значение, что нам и требовалось по условию задачи. Таким образом, мы нашли такие размеры кругового сектора и , при которых площадь бумажного змея наибольшая.

Другое о педагогике:

Особенности формирования связной речи у детей с нормальным речевым развитием
Связная речь представляет собой наиболее сложную форму речевой деятельности. Она носит характер последовательного систематического развернутого изложения, осуществляется в диалоге и монологе. Она включает в себя совокупность сложных постепенно формирующихся операций, умений, навыков, обеспечивающих ...

Конкретизация обучающих и когнитивных целей
Общая цель: дать основной материал по теме, сформировать, необходимые ЗУН у учеников. Обучающие цели: - Объяснить, что такое композиция; - Объяснить различия между объемной, плоскостной и пространственной композициями; - Объяснить, что такое симметрия, асимметрия, ритм, метр; - Показать примеры сим ...

Из истории изучения детской речи
Детская речь изучается в настоящее время разными науками. Наиболее часто детскую речь выделяют в качестве объекта исследования психология, психолингвистика и лингвистика, используя при этом свои, специфические методы, концентрируя внимание на каком-либо одном аспекте этого сложного явления. Речь ак ...