Реализация межпредметных связей отдельных разделов алгебры и начал математического анализа

Из этой таблицы следует, что на клеточку номер n нужно положить зерен, например, на клеточку номер 11 нужно положить зерен, а на клеточку номер 21 - зерен и т. д. Для того, чтобы подсчитать величину награды, мы должны сложить зерна, лежащие на всех клеточках шахматной доски:

Заметим, что есть 64 числа , которые образуют геометрическую прогрессию, первый член которой равен 1 , последний - и знаменатель q = 2. Сумма членов такой последовательности вычисляется по формуле:

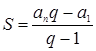
Применим к нашему случаю и получим:

Читается это гигантское число так: восемнадцать квинтиллионов четыреста сорок шесть квадриллионов семьсот сорок четыре триллиона семьдесят три миллиарда семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать. Такую награду должен дать царь Шерам изобретателю шахмат Сете. Представим себе тот объем, который занимает такое количество зерна. Известно, что 15000000 зерен пшеницы вмещается в 1 кубический метр. Разделив S на 15000000, мы получим, что награда должна занять 12 000000000000 м3 - двенадцать триллионов кубических метров. Для того, чтобы поместить такое количество зерна, достаточно, например, построить амбар, в основании которого лежит прямоугольник со сторонами 8 м и 10 м, а высота равна 150000000000 м = 15000000 км, что совпадает с расстоянием от Земли до Солнца! Совершенно ясно, что такого количества зерен нет ни у какого царя и выполнить просьбу Сете невозможно!

После того, как была рассказана эта легенда, можно переходить непосредственно к самой показательной функции.

Вернемся к количеству зерен, который нужно положить в клетку номер n шахматной доски. Обозначим это число через .Тогда

Таким образом, мы определили на множестве натуральных чисел функцию f , значения которой находятся по формуле: .

Заметим, что если некоторая величина на каждом шагу увеличивается вдвое, то она очень быстро возрастает. Такой рост характерен и для живых существ, если у них нет естественных врагов и достаточно ресурсов(пищи, воды, территории и т. д.). Например, когда однажды в Австралии оказалось на воле пара кроликов, то они размножались настолько быстро, что превратились в угрозу всему сельскому хозяйству страны.

Такие несложные примеры из различных областей знаний, которых можно привести множество, помогают учащимся осознать естественную необходимость существования и изучения понятия показательной функции.

Что касается второго способа, то есть показа применения изучаемого понятия в области предмета, являющегося профильным, то возможен такой вариант. После того, как будет введено число е, на занятии элективного курса нужно установить связь числа е с формулой сложных процентов.

Другое о педагогике:

Дидактическая игра как средство формирования операций логического мышления
Игра представляет собой особую деятельность, которая расцветает в детские годы и сопровождает человека на протяжении всей его жизни. Не удивительно, что проблема игры привлекала и привлекает к себе внимание исследователей, причем не только педагогов и психологов, но и философов, социологов, этногра ...

Общие данные о развитии лексики в онтогенезе
Вопросу развития лексики посвящено большое количество исследований, в которых данный процесс рассматривается в различных аспектах, таких как: психофизиология, психология, лингвистика и психолингвистика. Первоначально новое слово возникает у ребенка как непосредственная связь между конкретным словом ...

Особенности педагогического процесса в отечественной педагогике
педагогический профессиональный обучение деловой Анализ, отечественного опыта проектирования педагогической системы показал, что проекты разрабатываются представителями различных областей научного знания: педагогики, психологии, дидактики. Вопросы проектирования многоуровневой профессиональной подг ...